April 23, 2020

Another Look at Base Rate Fallacy for Shared Resources

—Logical fallacy and broken models.

Here’s another look at the base rate fallacy I discused in Logical Fallacy and Memory Allocation when applied to a shared resource. I’ll use memory allocation again.

This is a contrived example. I am not suggesting this anaylsis is correct. In fact, I’m trying to show the opposite (the fallacy of this approach).

Make sense?

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

df = dict()

Let $P(E = n)$ be the probability of the event occurring.

We know that $P(E = 1) = 1$, because this user initiated event must occur at least once in order to use the system.

Assume most users will have $n > 1$. Assume that $P(E = 2) = \frac{1}{2}$, $P(E = 3) = \frac{1}{3}$ and $P(E = n) = \frac{1}{n}$, for $1 \le n \le 300$.

The probability distribution function can be any function showing the probability of an event decreasing as the number of events increases.

def event_pdf(n):
    """Calculate the probability of the event occuring."""
    return 1 / n

df['P(E = n)'] = [ event_pdf(n) for n in range(1, 301) ]

for n in [ 0, 1, 2, 299]:
    print("P(E = {:3}) = {:1.3f}".format(n + 1, df['P(E = n)'][n]))

P(E =   1) = 1.000
P(E =   2) = 0.500
P(E =   3) = 0.333
P(E = 300) = 0.003

Let $P(C)$ be the probability of system memory being exhausted.

Then $P(C \vert E = n) = \frac{P(C) \cap P(E = n)}{P(C)}$.

Assume $P(C \vert E = n) = 0$ for all $1 \le n < 300$ and $P(C \vert E = 300) = 1$. That is memory exhaustion only occurs when $300^{th}$ event occurs.

(The careful reader will note the flaw here. While true the system crashes upon the $300^{th}$ event, it is wrong to consider this in isolation. But lets continue our argument with this flaw.)

def crash_given_event(n):
    """Calculate the probability of P(C|E = n)."""
    return 0 if n < 299 else 1

df['P(C|E = n)'] = [ crash_given_event(n) for n in range(0, 300) ]

We know $P(C \vert E = 1) = 0$ and $P(C \vert E = 300) = 1$.

for n in [0, 1, 2, 299]:
    print("P(C|E = {:3}) = {:1.3f}".format(n, df['P(C|E = n)'][n]))

$$P(C \vert E =   0) = 0.000$$
$$P(C \vert E =   1) = 0.000$$
$$P(C \vert E =   2) = 0.000$$
$$P(C \vert E = 299) = 1.000$$

Let $M(E = n)$ be the proportion of memory consumed at the completion of the $n^{th}$ event.

We know that $M(E = 300) = 1$ and $M(E = 1) = 0.75$. We know each event consums $0.0875$% of remaining memory.

def memory(n):
    """Determine percentage of consumed memory."""
    if 0 == n:
        return 0.75
    elif 299 == n:
        return 1
    else:
        return 0.75 + (n * 0.000875)
    
df['Memory (% Used)'] = [ memory(n) for n in range(0, 300) ]

We know that the system exhausts available memory immediately when the $300^{th}$ event occurs.

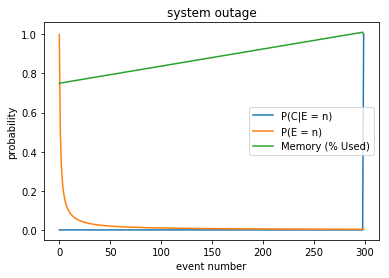
fig,ax = plt.subplots()

for name in ['P(C|E = n)','P(E = n)', 'Memory (% Used)']:
    ax.plot(df[name],label=name)
    
ax.set_ylabel("probability")
ax.set_xlabel("event number")
ax.set_title('system outage')
ax.legend(loc='right')

The system outage graph above is our model of the memory leak if we reason about the leak in isolation.

We can improve this model significantly and still make the same error.

def crash1_given_event(n):
    """Calculate the probability of P(C1|E = n)."""
    return 1 / (300 - n)

df['P(C1|E = n)'] = [ crash1_given_event(n) for n in range(0, 300) ]

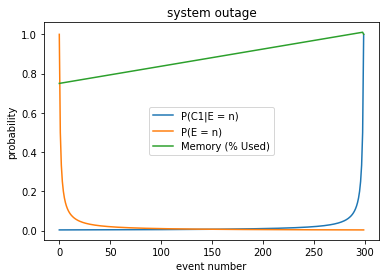
fig,ax = plt.subplots()

for name in ['P(C1|E = n)','P(E = n)', 'Memory (% Used)']:
    ax.plot(df[name],label=name)
    
ax.set_ylabel("probability")
ax.set_xlabel("event number")
ax.set_title('system outage')
ax.legend(loc='best')

The model $P(C1|E = n)$ considers the increase in probability of a crash as the number of events increases. Better, but flawed. Flawed because memory is a shared resource.

The model should look something like $P(C1 \vert E = n, F, G, \ldots)$, where $F$ and $G$ are other events affecting memory.

These models are positioned a probability distributions of different events in memory. These make for nice discussion points and reflect the fact that the underlying arguments are probability based.

In my opinion, a better approach is to count the bytes allocated and freed and map this over time and across different use cases.