A collegue recently provided me a link to Agile Release Trains (ARTs). It’s not an entirely new concept to me, but one that I’ve never had the opportunity to put into practice. ARTs are part of SAFe.

I view the release train model as separating scope from timeline–the idea that if your scope misses the nth train it can go into the nth+1 train. It’s a simple idea with possibly profound implications. SAFe uses ARTs as a key delivery vechicle. SAFe is much, much broader in scope.

To properly understand SAFe, take a look at the SAFe Principles.

A claim in Agile Release Trains is that ARTs are cross-functional. ARTs have all the capabilities—software, hardware, firmware—needed to define, implement, test, deploy, release, and where applicable, operate solutions.

ARTs operate on a set of common principles.

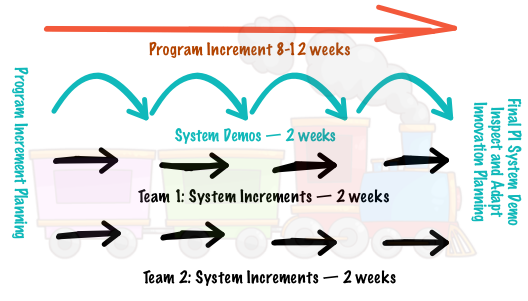
• A fixed schedule as determined by the program increment cadence. All agile teams use the same cadence. A program increment has a fixed length typically 8-12 weeks in duration.
• A system demo of each system increment every 2 weeks. A final system demo occurs at the end of each program increment. That demo includes the inspect and adapt activity.
• Has a known velocity for the program increment.
• Rely upon agile teams.
• Rely upon dedicated people who support the ART, regardless of their functional reporting structure.
• Rely upon face-to-face program increment planning.
• Provide a buffer for innovation and planning including dedicated time for
  • program increment planning,
  • innovation,
  • continuing education and
  • infrastructure work.
• Rely upon develop on cadance and release on demand, where demand is driven by a customer. ARTs apply cadence and synchronization to address the variability of Research and Development. Releasing is typically decoupled from the development cadence.

These principles interplay like this.

ARTs have some parallels with Scrum. Indeed, teams involved in ARTs may use Scrum.

The question is can ARTs be accomplished without SAFe? The short answer is they cannot.

The starting point for that question is Essential SAFe. You cannot separate ARTs from SAFe because ARTs are part of the key ingredients of SAFe. Those ingredients are:

1. Lean–Agile Principles
2. Real Agile Teams and Trains
3. Cadence and Synchronization
4. Program Increment Planning
5. DevOps and Releasability
6. System Demo
7. Inspect and Adapt
8. Architectural Runway
9. Innovation and Planning Iteration
10. Lean–Agile Leadership

If you want to use ARTs without SAFe you are really interested in a method like Scrum, Extreme Programming, or Kanban. The rationale for using ARTs is that they scale. And that’s the whole point fo SAFe: developing enterprise-scale solutions. The methods listed are focus on individual teams.

I found the interaction between Qt’s QSqlTableModel and composite primary keys difficult to understand. Those difficulties involved recurrent “No Fields to update” messages from QSqlError::lastError() when trying to insert. This post captures a small series of experiments to better understand the behavior. I started with a working example from the Qt Forum.

The code for this post is in a Git repository.

CREATE TABLE preferences(
    x TEXT NOT NULL,
    y TEXT NOT NULL,
    PRIMARY KEY(x, y)
    WITHOUT ROWID;

I’m using SQLite (3.28.0 2019-04-16 19:49:53 884b4b7e502b4e991677b53971277adfaf0a04a284f8e483e2553d0f83156b50) and qt 5.13.0.

Each change to bring the table in the example closer to my ideal is on a separate branch. This permits a simple diff between the master branch and the changed branch to determine the alterations I’ve made to the original example.

Branches

* fb8951a -  Converted composite primary key types to text (introduce_text_fields)
* 205492f -  Introduced constraints on composite primary key (constrained_composite_primary_key)
* c2f67c0 -  Introduced an unconstrained composite primary key (composite_primary_key)
* 184f5ed -  Removed QCoreApplication (master)
| * d731611 -  Converted ROWID table to a table (without_row_id)
| * 5dcc914 -  Removed QCoreApplication 
|/  
* ec024b1 -  White space change 
* 3bd46af -  Download of original source code 
* 2fe4f3e -  Initial commit

Conclusion

The table structure is not the problem.

Turns out a critical component of the code was missing:

 QSqlTableModel model(0, database());
 model.setTable("rast123");
 model.select();
 model.database().transaction();

Initialization of the QSqlTableModel was being done in a constructor. For some reason, this needs to be done again to prepare for the row insert. Doing so with the methods attached to this don’t have the desired effect.

I recently experimented with Qt and QML in an effort to construct an application that relies upon a QML ListView and a C++ model. This is a collection of resources that I found helpful. Article relies upon Qt 5.12.

I wandered around in the dark on some of this. The best path forward for learning is item 2 and 3.

Item 1 was my reviewing the difference between Model-View-Controller and the Model Delegate used by Qt.

Item 4 looks at whether I need to implement insertRows() when I found Qt’s documentation on subclassing QAbstractListModel a little vague. (I don’t.)

The winding path:

1. A terrific Model View Controller (MVC) diagram provides a simple explanation of the Model-View-Controller pattern. This includes a diagram and a set of rules that are well presented and straight forward to understand.

   The nice part of this article is that it shows best practice and poor practice side-by-side.

2. Models and Views in Qt Quick provides an overview on models and views in Qt. Qt uses a variant of MVC that combines the view and controller into a single entity and introduces a delegate. Importantly, the delegate is not a controller.

   There is some confusion regarding Qt’s implementation of MVC (see for example Why Qt is misusing model/view terminology?). That thread was useful to provide a contrast to a textbook MVC implementation.

   For me the answer lies in whether you choose to separate the view and controller. (My favorite reference for Model View Controller.) Qt combines them to create a Model Delegate pattern. The model delegate pattern combines the view and controller into a UI delegate.

3. Using C++ Models with Qt Quick Views has a video showing how to create an application with QML and a C++ model.

   Explanation on creating read-only view and extending them to C++ models (around 9:31).

   The video shows how to connect the view and model together using a delegate in C++ (around 13:00 through to the end of the video).

   Importantly, the view (a QML ListView) is connected to the model in C++ (the TodoModel class) using the QML model keyword. The model is connected to the data, also in C++ (the ToDoList). The creation of the TodoList class starts at 20:30.

4. Address Book Example provides a look at using a QTableView (my goal was a QListView). This example proved helpful in understanding whether the insertRows() method needed to be implemented or not. This example provided a look at what an implementation should look like.

   By default, insertRows() returns false if it’s not overloaded in a subclass of QAbstractListModel. The guidance in QAbstractListModel is you can overload this method (of course you can). It was light on details as to when you had to overload it.

Thinking about the QML and C++ model in terms of a Model Delegate instead of Model-View-Controller permits better reasoning about the implementation.

A source of confusion for me was the relationship between the QML QListView and the QAbstractListModel as it relates to model updates. Using C++ Models with Qt Quick Views puts the data in the backend, separate from the model (see video at 30:11). It follows the guidance in Models and Views in Qt Quick. Whereas, How to Use a QSqlQueryModel in QML puts data in the model’s constructor (see step 4 [implementation] and step 3 [use]).

The difference between the two approaches is unclear to me at this time. It’s unclear because I view the database as a persistent data store similar in purpose to the TodoList class in Using C++ Models with Qt Quick Views. Not sure why the rules would change.

(To be fair, when I wrote this article How to Use a QSqlQueryModel in QML was tagged as needs improvement.)

Here’s a list of starting points in the video from Using C++ Models with Qt Quick Views:

The only confusing part of the video was the introduction of data into the constructor of the ToDoList class at 45:30. The ToDoList class looks like it’s part of the control. It’s a small point, especially in a tutorial, but adding data to ToDoList gives that class multiple reasons to change. In my opinion, a better approach is to extend ToDoItem to include a container class and have ToDoList use that container instead.

In Working Agreements as Principles, I discuss my continued belief that good working agreements are principles and provide an example on why. I’ve long suspected that this approach eventually leads to uncovering a team’s values as well.

I’ve been using the working agreement as a principle with the last two software teams I worked with. Their use with the first team, lead to the personal realization that I value good code review above some other activities. The second team took 14 months to get from principle to values in relation to code review. I believe that the introduction of BitBucket and transparency around code review prompted this change. (Both teams used BitBucket, although the first team started with Review Board.)

So here I am. Fourteen months after the introduction of the working agreement on code review I am about to embark on a discussion on values. Here’s out I’d like the discussion to play out:

• Reiterate the working agreement. Our working agreement permits 2 or more reviewers to have a veto on merge to master and requires the author and reviewers work out differences.
• Point out that the working agreement in intended to protect the master branch
• Reiterate the importance of working agreement as a princple. Emphasize that merge to master without code review is discouraged, but if the reviewers think its appropriate then do it. If code review is a principle we adhere too then this should make people uncomfortable but their might be circumstances where it’s deemed appropriate.

The rationale for the contradiciton between “protecting” master and having reviewers give a ship it without review needs some explanation.

The contradiction is important to get people to express their belief. I want people to think “yeah, we could but should we?” In my view, it’s an important element of getting people to think about what they are doing.

In my situation, I have a situation where one person is merging a lot of code to master without review because we are bootstrapping a new implementation. This is making many people on the team nervous, as well it should. We are breaking basic Agile principles (particularly the one about working code) and our working agreement. But are we doing it for a good reason? Possibly. But that’s where the values and principles come in.

My hope is that the team will start to discuss their differences in relation to the working agreement. My hope is that the value conversation will drive better decision making. Decision making like: we should never do this under any circumstance or this situatin is unusual and it’s ok for a while.

Either way, it will be a great opportunity to see how the team’s bought into code review. And we might learn something about the “why” of how we build software together.

I’m hopefull about this dicussion.

I recently took a tour of several programming languages. The objective was to try to implement the same solution in Rust, Haskel and Clojure. The important part of this exercise was that I hadn’t written anything in any of these languages previously.

I have to say that I really like Rust and the philosophy embodied in how that language approaches things. For example, using Cargo meant that I didn’t need to mess with a build system. With C++ I usually gravitate toward GNU Make or CMake both of which I’m beginning to find are a distraction from the implementation.

The most interesting thing that came out of my experience with Rust was their approach to structures and getters or setters.

One of the problems I have with a lot of C++ code is that the default impluse seems to be to create everything as a class. I prefer to use struct for certain things–usually PODs (Plain Old Data) but with an eye towards how the structure fits into the domain. The idea is that you start with a struct and build up your implementation until you have a strong case for a class.

For example, building up a data structure for managing people might look like this:

struct Person {
   string name;
};

A Person contains a collection of attributes describing a person. Those attributes might reside in a persistent store, such as a database.

struct SelectablePerson: Person {
   bool isSelected;
   SelectablePerson()
       : Person()
       , isSelected(false) { }
};

A SelectablePerson extends a Person to include a selected attribute. This attribute might be represented in a view where the person is selected (included) in a query against the database. The constructors are for convienience and ensure a consistent state for creating selectable people.

In C++, the argument for using a class starts to look appealing because the constructor is starting to push the boundary of a POD. In Rust, your choice is to develop traits to apply to Person. I’m going to take the position that SelectablePerson should remain a struct in C++. That argument rests in the Single Resposibility, Open-Closed and the Liskov Substitution principles (the SOL in SOLID).

In C++, a lot of people will argue you want getters and setters for the name and isSelected attributes. This usually drives them down the path of a class because of member visibility rules (i.e., make these attributes private). I’ve also had arguments with C++ programmers who insist that data members in a class be public because they don’t want to write getters and setters.

Rust has a different approach. By default, stucture members are private and you need to add the pub attribute to make them visible. What surprised me was that a lot of Rust examples forego getters and setters in favour of direct access if you make the attribute public.

The argument in favor of using a getter and setter is encapsulation. You can change the attribute without affecting clients. The counter argument is that the difference between

Person p;
p.name = "brian";

and

Person p;
p.set_name("brian");

isn’t significant. It isn’t significant because the logic surrounding this is just where you want the assignment statement. The first example, puts this assignment in every client class; the second does not.

Rust falls into the first example.

Importantly, I’m not saying you should open up your data members everywhere. I’m saying there is a time and a place for it and you shouldn’t just blindly make everything a class in C++.

Here’s an example where I think a class is appropriate.

class PeopleContainer {
public:
    /*! Container for SelectablePerson. */
    typedef std::vector<SelectablePerson> ContainerType;

    /*! @brief Construct the controller.
     */
    PeopleContainer()
        : container()
        , selected_count(0) { }
private:
    ContainerType container; //< A container for selectable people.
    size_t selected_count; //< A count of the number of people currently selected.
};

Why am I using a class here? The selected_count member requires additional logic to ensure that the number of SelectablePerson.isSelected values set to true is equal to the count. Neither Person nor SelectablePerson have this constraint.

In Rust, I’d introduce a countable trait to create an equivalent construct for the PeopleContainer.

So how did Rust improve my C++? It gave me a better understanding on why I was using struct instead of class in C++. It gave me a better understanding of the importance of SOLID in C++, particularly the Liskov Substitution principle. An important element of Liskov Substituion is type inheritance, not implementation inheritance. There is only type inheritance in these examples.

In all, I’m back to using C++ but I have only good things to say about Rust and look forward to the next opportunity to explore it.